Batch 3 - Class 220 - Leibniz' Triangle
Attendance: Shikhar, Vansh, Aarkin, Ayush, Advay, Kabir
Class Notes: (Repeat from class 95)
- Play the following puzzle on an infinite triangular array (only the first six rows are shown here). The puzzle begins with three coins placed at the apex of the array and a move consists of removing a coin from the array that has two empty cells just below it and replacing it with two coins in those empty cells. For example, two moves to start the game are shown.
.png)
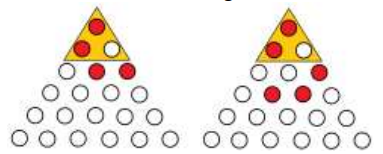
The object of the game is to empty the top three cells of the triangle of coins. How many rows of the triangle do you need to accomplish the task?
- Let kids attempt for a while. Some kids may come to the conclusion that it seems to go on. How can we prove that this is not doable?
- Introduce Leibniz' Harmonic Triangle. Unlike Pascal triangle, where any circle has a number which is sum of two circles above it, Leibniz' Triangle circle has a number which is sum of two circles below it. Ask kids to construct a sample Leibniz' Triangle.
- If they have not got to the 1,1/2,1/4 Leibniz triangle, help them get there. Now do you see a solution?
- What is the invariant here when we make a move?
- At any stage of the game, what should be the total of all covered cells?
- What is the possible total besides the top three cells? How many moves does it take to create a total equal to top three cells?
- Answer: In any finite number of moves, it is not possible to get to total of 2 without having one of the top three cells covered.
- Can it even be done in infinite moves? What are the kind of patterns that develop as we "roll out" the coins? How does the triangle fill up at the edges relative to the center?
- Introduce the "real" Leibniz' Harmonic Triangle, which is reciprocals of Pascal triangle multiplied by 1/n for nth row. Notice that this has the same property and hence our coin game will work on this triangle as well.
- But, what is the sum of left edge here (1/1+1/2+1/3+1/4 ... = infinite), which means that if we desire a sum of two then we can't go on infinitely on edges, so we need to go "more than infinite" in the center!?!? In fact 1/3+1/4+1/5...1/19 > 2.
Homework
- (Moscow - 174) Wheels A,B,C and D are connected with belts as shown. If wheel A starts to rotate clockwise, can all the 4 wheels rotate? In which direction would each wheel rotate?
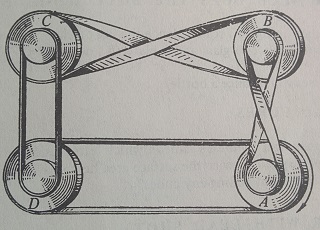
- Can the wheels rotate if all 4 belts are crossed?
- What is belt 1 and 3 are crossed?
References:
The Moscow Puzzles, by Boris A. Kordemsky